Tym razem chciałbym podzielić się tym, czym jest rewolucyjne podejście. Oznacza to pewien przełom, przeskok czy też niespotykane odkrycie w danej dziedzinie... takie, którego nikt się nie spodziewał. W żargonie internetowym, można byłoby wręcz powiedzieć mocno żartobliwie: "nikt nie prosił, a dostaliśmy {to o czym zawsze marzyliśmy}".
Dlaczego chcę zaprezentować coś czego w zasadzie nie widuję jako tak zwane dobre praktyki? Może dlatego, że nie umiem szukać, a może dlatego, że coś takiego jest tylko dla elitarnej grupy, która nie dzieli się swoimi pomysłami z tak zwanym światem zewnętrznym? Są różne powody, ale nie mnie ich dociekać. Ja chcę pokazać coś, co może innym pomóc w zrozumieniu kilku kwestii, a może i odważeniu się na to, aby zrobić coś co pomoże im przejść na koleny poziom.
Podzielę się swoją prezentacją i omówię krok po kroku. Do tego też dodam, co jest niezbędne, aby mieć możliwość zaprezentowania jej przed szerszym gronem.
1. Pomysł na prezentację: coś co twoim zdaniem jest fajne, ciekawe, niezwykłe, oryginalne i wartościowe. Nie ma znaczenia czy ktoś kiedykolwiek już tym się dzielił, ale ma znaczenie to na ile ty uważasz, że świat powinien się o tym dowiedzieć. I to nawet ten świat, który składa się z kilku, kilkunastu czy kilkudziesięciu odbiorców.
2. Opracowanie od strony merytorycznej i technicznej. Krótko mówiąc, sprawdzenie czy wszystkie koncepcje, którymi chcesz się podzielić są ze sobą spójne. Dobrze byłoby, aby również były wynikowe oraz pokazujące coś, czego inni zdają się albo nie dostrzegać, albo nie rozumieć... albo też nie stosować.
3. Znalezienie odbiorców i platformy dzięki której zaprezentujesz, to co uważasz za ważne, ciekawe, wartościowe a może i nawet inspirujące. Odbiorcami mogą być ludzie, którzy dowiedzą się o tym kiedy i gdzie będziesz to prezentować (w domyśle online), a także na jakiej platformie będzie można to podziwiać (tutaj do wyboru są powiedzmy tak zwane lajwy (transmisje na żywo) w różnych social mediach, a dodatkowo z wykorzystaniem takich jak: YouTube, Twitch, Teams, Google czy też poprzez plaformę Zoom).
I teraz z mojej perspektywy i doświadczenia. Od kilku lat tworzę artykuły związane z nauczaniem matematyki, tak aby w końcu odczarować matematykę jako tę nieszczęsną, niezrozumiałą oraz będącą źródłem wiecznego cierpienia wielu uczniów (niestety nie jest to wyłącznie metafora).
Na przestrzeni dwóch lat zajmowałem się takimi zagadnieniami jak: wysokość, proste równoległe i prostopadłe, trójkąty, czworokąty jak też przekątne. Do tego częściowo także obracanie i łączenie figur jak też twórcze podejście do zrozumienia istoty wielokątów, zwłaszcza tych foremnych, które w pewnym uproszczeniu (gdy ich liczba kątów dąży do nieskończoności) mogą być kołem (okręgiem). Przy okazji także tematy kątów, boków oraz definicji jak też właściowości podstawowych czoworokątów. W sumie trochę się tego uzbierało.
Na podstawie tych analiz i opracowań doszedłem do punktu w którym uznałem, że dobrym pomysłem byłoby to zebrać do kupy i spróbować pokazać czworokąty w takiej perspektywie w jakiej jeszcze nigdy nie widziałem. Dla wielu osób będzie to banalne i oczywiste, ale dla mnie akurat takie nie jest. Dlaczego? Ponieważ obserwuję różne pomysły nauczycieli matematyki, którymi się dzielą (w przestrzeni grup matematycznych na FB) i jak dotąd czegoś takiego nie widziałem. Postanowiłem zatem zebrać wszystkie zagadnienia w taki sposób, aby zaprezentować nowe i jak dla mnie rewolucyjne podejście do tego tematu.
Na czym ma polegać rewolucja? Na tym, że uczymy się o człowieku nie o oderwaniu od całości, tylko z uwzględnieniem wszystkich systemów, ale pokazując jak wzajemnie się one przenikają i co z tego wynika. Rzecz jasna moje rewolucyjne podejście musi być wyjściem do jeszcze lepszego opracowywania zagdanień, które sprawiają wielu dzieciom problemy. Ja tylko pokazuję, że obecny poziom tego jak nauczamy o wielokątach jest po prostu niewystarczający względem potrzeb i możliwości dzieci (rozwojowych, intelektualnych jak i percepcyjnych).
Spieszę dodać, że oczywiście zdaję sobie sprawę, że klasy są przeładowane, wiele dzieci ma różne orzeczenia jak i zaburzenia zachowania. Jednak ja mówię o merytorycznym i twórczym, a jednocześnie holistycznym (całościowym) podejściu do nauczania myślenia na bazie matematyki (w tym momencie na czworokątach), a nie o trudnościach (lub niekiedy braku sensu) w realizacji procesu edukacyjnego. Zatem tę kwestię mamy wyjaśnioną, więc lecimy dalej.
Czy moja prezentacja może być postrzegana jako matematyczny projekt?
Prezentacja pomimo, że wygląda dość prosto, to zawiera wiele pomysłów i zagadnień, które są przez dzieci przyswajane i utrwalane niejako mimochodem. Inaczej mówiąc, uczą się czegoś co często formalnie będzie wyjaśniane na późniejszych etapach edukacyjnych.
Z czego składa się prezentacja i dlaczego może być przełomem w nauce matematyki?
Prezentacja składa się z 4 pomysłów i części dodatkowej (bonus). Poniżej krótkie streszczenie.
STRESZCZENIE prezentacji: "Odkrywanie i budowanie podstawowych czworokątów: nowe podejście"
Właściwości podstawowych czworokątów są bardzo szybko zapominane przez uczniów. Jednym z powodów jest brak zrozumienia ich właściwości spowodowany mechanicznym uczeniem się na pamięć. Budowanie i odkrywanie czworokątów z wykorzystaniem koncepcji torów, wzajemnych relacji przekątnych jak też łączenia różnego rodzaju trójkątów znacząco pomaga w zrozumieniu oraz utrwaleniu ich właściwości.
Koncepcja torów wykorzystuje dwie proste równoległe, które stanowią bazę do wyznaczania podstaw figur. Bazując na niej tworzymy odcinki różnej długości i różnego przesunięcia względem siebie, co pozwala lepiej zrozumieć istotę prostych równoległych i prostopadłych, a przede wszystkim - znaczenie wysokości.
Przekątne są odcinkami, które mogą przecinać się w różnych miejscach, ale zawsze mają punkt wspólny. Odcinki mogą być tej samej lub różnej długości. Ponadto te odcinki przecinają się w różnych miejscach i pod różnym kątem. Jeśli przecinają się w swoich połowach pod kątem prostym, to mogą powstać tylko dwie figury. Natomiast jeśli zmienimy położenie przecinających się odcinków, tak aby nie były prostopadłe do siebie - utworzymy kolejne dwie.
Trzecia koncepcja polega na tym, że budujemy cztery podstawowe czworokąty za pomocą kombinacji różnych trójkątów: równoramiennych, równobocznych, prostokątnych, ostrokątnych i rozwartokątnych. Ta zabawa obiektami pozwala na głębsze zrozumienie i utrwalenie właściwości zarówno czworokątów jak i trójkątów. Temat pól figur nabiera nowego wymiaru, ponieważ możemy sami manipulować obiektami, sprawdzając różne ich kombinacje ułożenia. Składanie i rozkładanie figur z różnych części pozwala dostrzegać również zależności pomiędzy przekątnymi jak i kątami.
Ostatni pomysł to połączenie szachowych idei z interesującymi ciągami: arytmetycznym i geometrycznym. To jest przejście na kolejny poziom, który sprawia, że proces odkrywania staje się coraz bardziej wciągający i jednocześnie stanowiący wyzwanie. Zaczynamy od siatki 8x8 (przypominającej szachownicę, ale bez kolorów pól) i sprawdzamy co się dzieje, gdy małe kwadraty są dodawane jeden do drugiego. Możemy dzięki temu zauwazyć interesujące relacje pomiędzy kwadratami 1x1, 2x2 i 3x3. W międzyczasie uczymy się jak generować pomysły i odkrywać właściwości związane z ciągami arytmetycznymi i geometrycznymi (oraz ich sumami). W końcu bawimy się warstawami i widzimy różne konfiguracje trójkątów, które zawierają 2, 3 lub 4 trójkąty prostokątne równoramienne ("półkwadratusy").
Część dodatkowa (bonus), to pytanie o twórcze modyfikacje twierdzenia Pitagorasa. Najpierw uczymy się na konkretach (poprzez wycinanie) o klasycznych twierdzeniu Pitagorasa, w którym suma dwóch KWADRATÓW opartych na (przyprostopkątnych) bokach trójką prostokątnego, jest równa sumie KWADRATU zbudowanego na przeciwprostokątnej (czyli najdłuższym boku).
Na bazie tego klasycznego podejścia stawiamy kolejne pytanie (a wraz z nim nożyczki i możliwość testowania na konkretach), czy ta sama zależność będzie występowała w przypadku, gdy na tym samym trójkącie prostokątnym:
a) zbudujemy trójkąty prostokątne równoramienne na wszystkich bokach tego trójkąta
b) zbudujemy trójkąty równoboczne na wszystkich bokach tego trójkąta
Dzięki temu możemy dawać dzieciom okazję ku temu, aby same odkrywały i tworzyły to, czego się później będą uczyły jako formalne treści matematyczne (w tym podstawy dowodzenia).
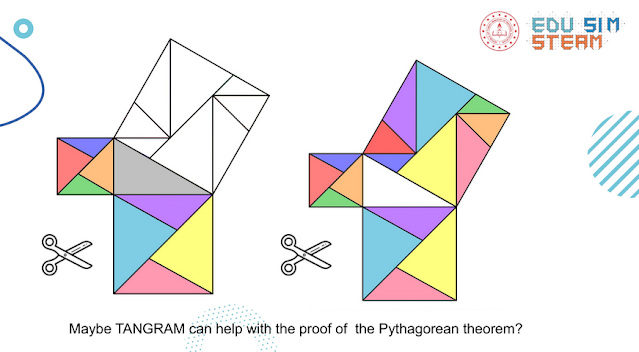
Na koniec pytamy dzieci czy są w stanie za pomocą TANGRAMU pokazać, że klasyczne twierdzenie Pitagorasa, może być wykazane poprzez dowód (tak, dostosowujemy poziom trudności do możliwości dziecka) w postaci zmieszczenia wszystkich trójkątów jako ułożenie największego kwadratu. Nie znam dziecka, któremu sprawi to jakiekolwiek trudności oraz takiego, które nie będzie ciekawe to czy działa (tzn. czy te małe trójkąty można ułożyć tak, aby powstał duży kwadrat).
Manipulacja i zabawa oparta na tych trzech pomysłach dają możliwości widzenia i doświadczania procesu tworzenia figur z różnych perspektyw. To z kolei powoduje znaczne lepsze przyswojenie niezbędnych właściwości tych figur. Osiągamy to za pomocą połączenia różnych koncepcji, na bazie zabawy, manipulacji, odkrywania jak też budowania. Przy okazji do realizacji tego celu możemy tworzyć różne konfiguracje pracy uczniów w większych lub mniejszych grupach, tak aby wykorzystać uczenie się rówieśników.
Tyle tytułem streszczenia. Teraz w skrócie powiem o tych koncepcjach i o tym jak mogą być wykorzystane.
KONCEPCJA 1: Tory.
Na ich podstawie możemy pomóc dzieciom zrozumieć znaczenie prostych równoległych. Warto krótko podyskutować o tym co by się stało, gdyby tory nie były równoległe: jak wpłynęłoby to na podróż pociągiem?
Następnie mamy kwestię linii równoległych, prostopadłych oraz wysokości. Po czym rozpoznać, że dwie linie są równoległe? Jak szybko zorientować się, że nie są? Jaki niezbędny warunek musi być spełniony, aby rozumowanie było prawidłowe (poprawne)?
W przypadku prostokąta rysujemy czerwoną ramkę (to nasze tory), która będzie szablonem stosowanym do pozostałych czworokątów.
W prostokącie zaczynamy od narysowania wysokości (od dolnej podstawy), która jest prostopadła do obu torów. Następnie rysujemy tą samą długość na dolnej jak i górnej podstawie, a potem łączymy prawy bok prostokąta (oba wierzchołki). Warto podkreślić, że jeśli górna i dolna podstawa nie będą tej samej długości, to nie będzie wszystkich kątów prostych, a zatem nie otrzymamy prostokąta.
Teraz kolej na kwadrat. W kwadracie wszystko robimy tak samo jak w prostokącie, ale z jednym wyjątkiem: długość górnej i dolnej podstawy musi być taka sama jak długość wysokości. I na tej podstawie możemy stwierdzić i zapamiętać, że kwadrat jest prostokątem, który ma wszystkie boki równe. Prawda, że proste? Nie tylko proste, ale i wynikowe! To jest jeden z kluczy do sukcesu w nauce matematyki.
Następnie mamy do narysowania nasz równoległobok. I znowu bazujemy na prostokącie (od którego zaczęliśmy). Prosimy nasze dzieci, aby tym razem narysowały odcinek, który jest podobny do wysokości, ale nie jest prostopadły do żadnej z podstaw. W ten sposób dzieci zaczynają dostrzegać nachylenie odcinków oraz intuicyjnie czują to, czym są kąty. Za jakiś czas możemy do tego wrócić, gdy będziemy uczyli się o kątch przyległych, wierzchołkowych, naprzemianległych i im podobnych. I gdy już narysujemy pochyły odcinek, biegący od dolnej do górnej podstawy, wówczas rysujemy dłuższy od niego odcinek będący podstawą górną i dolną. Przy czym podkreślamy wyraźnie, że obie podstawy muszą być tej samej długości. Jeśli tak się stanie, wówczas łączymy prawą stronę naszego równoległoboka, tak aby powstało prawe ramię (łączymy oba wierzchołki). I dzieci powinno niebawem zorientować się, że kąty nachylenia obu ramion są takie same. Tak, to właśnie jest odkrywanie własności figur! Możemy powiedzieć, że nasza figura jest dość podobna do prostokąta, ale różni się tym, że jej ramiona nie są prostopadłe do obu podstaw (chociaż mogą być, ale wtedy mieliśmy prostokąt).
Przejdźmy teraz do rombu. Co robimy? Przypominamy sobie właśnie co powstały równoległbok i różnica tym razem polega na tym, że długość (lewego) ramienia musi być taka sama jak długość każdej z podstaw. I po połączeniu trzech boków, pozostaje nam czwarty: prawe ramię, które również ma tę samą długość, co każdy z pozostałych boków. Okazuje się, że dzieci również powinny dostrzec to, że ramiona są pochylone pod tym samym kątem, a do tego kąty naprzeciwko siebie są takie same, czyli tej samej miary (jak kto woli: tak samo rozwarte).
Pora na trapez. W przypadku (klasycznego/tradycyjnego) trapezu mówimy dzieciom, że zaczynamy tak samo jak z rombem, ale po tym jak narysujemy pochylone prawe ramię, następnie rysujemy górną podstawę dłuższą niż nasze ramię, a następnie dolną podstawę znacznie dłuższą niż każdy z dwóch boków (idealnie, aby była dłuższa co najmniej dwukrotnie od górnej podstawy). Dopiero po tym dokańczamy rysowanie prawej strony trapezu (łączymy wierzchołki odcinkiem, który tworzy prawe ramię). No i powstaje nasz trapez. Jeśli dobrze wykonaliśmy rysunek, to powinno być widoczne gołym okiem, że żadne z ramion nie są tej samej długości, a nawet to, że wszystkie boki są różnej długości! I dzięki temu mamy trapez różnoboczny i odkrywamy właściwości (a także cechy wspólne i różnice), na bazie których możemy później budować kolejne odmiany figur (trapez równoramienny i prostokątny).
KONCEPCJA 2: Przekątne.
Na początek dajemy dzieciom możliwość narysowania różnych odcinków łączących dwa dowolne wierzchołki (nie należące do tego samego boku). Dobrze jest dać dzieciom kilka różnych figur, aby same poczuły to czym są owe przekątne. Zaczynamy od trójkąta, potem kilka różnych czworokątów (także tych nieregularnych, byle nie wklęsłych), a następnie, pięciokąt, sześciokąt i powiedzmy 8 lub 10-kąt. W zależności od dostępnego czasu i możliwości, dzieci mogą następnie (lub na końcu zajęć) narysować oraz policzyć wszystkie przekątne w każdej z figur (lub w kilku wybranych). Tak, za jakiś czas będzie jak znalazł jeśli chodzi o wielokąty (nie tylko forme) i to w jaki sposób zrozumieć wzór na liczbę przekątnych w wielokącie (jak i wzór na kąt wewnętrzy i sumę wszystkich kątów!). Po tym jak dzieci już poczują sens przekątnych można je zapytać o to czy w każdej z figur są one równej długości oraz od czego zależy to która z nich jest dłuższa a która krótsza.
Następnie testujemy przekątne, aby zobaczyć jakie figury powstaną.
I. Przekątne prostopadłe:
a) tej samej długości
b) różnej długości
I teraz mogą one przecinać się w swoich połowach, a gdy są tej samej długości, to powstaje nam kwadrat, zaś gdy przecinają się w tych samych proporcjach, to otrzymujemy trapez równoramienny.
Natomiast gdy przekątne przecinają się w swoich połowach, ale są różnej długości, to powstaje nam romb, zaś gdy przecinają się w tych samych proporcjach, to otrzymujemy czowrokąt nieregularny (na rysunku zaznaczony dwoma czerwonymi znaki zapytania).
Z naszej tabeli wynika, że deltoid otrzymamy w dwóch wypadkach:
1) wtedy, gdy przekątne są prostopadłe i SĄ RÓWNEJ długości oraz tylko jedna przekątna przecina się w swojej połowie
2) wtedy, gdy przekątne są prostopadłe i NIE SĄ RÓWNEJ długości oraz tylko jedna przekątna przecina się w swojej połowie
Warto podkreślić, że przecięcie się jednej przekątnej w swojej połowie sprawia, że jedna z nich jest symetralną drugiej.
II. Przekątne nieprostopadłe:
a) tej samej długości
b) różnej długości
I teraz mogą one przecinać się w swoich połowach, a gdy są tej samej długości, to powstaje nam prostokąt, zaś gdy przecinają się w tych samych proporcjach, to otrzymujemy trapez równoramienny.
Natomiast gdy przekątne przecinają się w swoich połowach, ale są różnej długości, to powstaje nam równoległobok, zaś gdy przecinają się w tych samych proporcjach, to otrzymujemy czowrokąt nieregularny (na rysunku zaznaczony dwoma czerwonymi znaki zapytania).
W przypadku dwóch pozostałych możliwości (podwójne znaki zapytania nad sobą) również otrzymamy czowrokąt nieregularne.
* - warto przyjąć następującą definicję deltoidu: czworokąt, którego przekątne są prostopadłe i jedna z nich jest symetralną drugiej. Dzięki temu wszystkie elementy i własności w naszej tabeli będą w pełni poprawne i zrozumiałe.
Na podstawie tych eksperymentów z przekątnymi, dzieci będa w stanie bardzo szybko przyswoić sobie podstawowe właściwości związane z przekątnymi związanymi z prostokątem, kwadratem, równoległbokiem i rombem. Wszystkie z tych figur mają bowiem przekątne przecinające się w swoich połowach bez względu na to czy są prostopadłe czy nie. Jeśli są prostopadłe to mamy do czynienia z kwadratem lub rombem, zaś jeśli nie są - z prostokątem lub równoległobokiem.
Warto również podkreślić, że dzieci w procesie tworzenia figur na bazie czworokątów mogą odkryć, że otrzymają trapez równoramienny tylko wtedy, gdy przekątne są równej długości i przecinają się w tej samej proporcji - bez względu na to czy obie przekątne są prostopadłe czy nie.
Kolejnym elementem prezentacji jest tabela. Zawiera ona wszystkie właściwości czworokątów, do tego definicję oraz łatwe możliwości porównywania i grupowania.
Przykładowo w wierszach (poziomo) mamy wszystkie właściwości danej figury. Na zielono mamy opcję "TAK", zaś na czerwono opcję "NIE". Możemy zobaczyć, że przykładowo w czwartym rzędzie mamy romb, który ma cechy nr 3 i 4, natomiast w pierwszym rzędzie prostokąt, który ma cechy 1 i 3. Warto podkreślić, że wszystkie figury w tabeli mają cechę nr 5, ponieważ wszystkie należą do grupy trapezów (co najmniej jedna para boków równoległych). Dodatkowo jeszcze w tabeli mamy ukrytą definicję każdej z figur. Znajduje się ona na przecięciu tego samego wiersza i kolumny - czy na przekątnej 1-1, 2-2, 3-3, 4-4 i 5-5. Przyznam, że to jest tabela nad którą pracowałem dość długo: zawiera wszystkie niezbędne własności figur, ich definicję a jednocześnie pozwala grupować figury pod względem wspólnych cech czy też ich braku.
KONCEPCJA 3: Łączenie różnych trójkątów i czworokątów.
Na początek bierzemy trójkąt różnoboczny: nieco dokładniej dwie identyczne sztuki takiego trójkąta. Następnie łączymy je bokami o długościach: najkrótsze, średnie i najdłuższe. I dzięki łączeniu tych figur obserwujemy jakie figury powstają.
Później rysujemy wysokość, która pada na każde z boków, które wcześniej wymieniliśmy. Kolejny krok, to rozcięcie nożyczkami wzdłuż tej linii (wysokości) i przyłożenie (można przykleić taśmą przezroczystą) z drugiej strony, tak aby za każdym razem powstał prostokąt. Na bazie tego ćwiczenia dzieci uczą się intuicyjnie zagadnienia pola figur. Stopniowo pytamy dlaczego rozcinaliśmy wzdłuż wysokości, a także dlaczego wysokość musi być prostopadła do podstawy (boku) na którą pada. To wszystko sprawia, że dzieci rozumieją każdy najmniejszy krok w procesie tworzenia wzoru na pole figur.
Dalej mamy prostokąty. Również bierzemy dwie identyczne sztuki i przykładamy do siebie najpierw krótszymi bokami, a później dłuższymi.
W przypadku połączenia krótszymi bokami zawsze otrzymujemy prostokąt, natomiast po połączeniu dłuższymi niekiedy możemy otrzymać kwadrat. I znowu jest okazja do dyskusji nad tym od czego będzie zależeć to czy powstanie kwadrat czy też prostokąt. Podpowiedzią jest oczywiście zagadnienie wielokrotności: jeśli suma dwóch krótszych boków będzie równa długości dłuższego, wówczas po połączeniu obu prostokątów dłuższym bokiem otrzymamy kwadrat. W przeciwnym wypadku zawsze będzie to prostokąt. Na rysunku obok widzimy co by się stało, gdybyśmy łączyli 4 prostokąty - jeden nad drugim. Wtedy suma czterech krótszych boków musi być różna dłuższemu bokowi prostokąta: tylko wtedy otrzymamy kwadrat. Mam nadzieję, że dzięki temu dzieci również zaczną postrzegać zagadnienia wielokrotności (a przy okazji stopniowo także proporcji) w innej perspektywie.
Co się dzieje, gdy łączymy dwa kwadraty ze sobą? Odpowiedź jest prosta: otrzymujemy zawsze prostokąt. I to bez względu na to którymi bokami połączymy oba kwadraty.
Na kolejny ogień idą trójkąty, ale tym razem prostokątne. Znowu bierzemy dwie identyczne sztuki i manipulujemy. Na początek oba łączymy najkrótszymi bokami, potem dłuższymi (czyli obiem przyprostokątnymi), a na końcu najdłuższymi (przeciwprostokątnymi).
Przy połączeniu najkrótszymi bokami otrzymujemy albo trójką równoramienny albo równoległobok. Jak skleimy trójkąmy dłuższymi, wówczas znowu te same możliwości, a gdy najdłuższymi - wówczas magicznie wyskoczy albo prostokąt albo deltoid (przez dzieci często nazywamy latawcem, jako że jego wygląd w pełni na to zasługuje). I znowu można zadać pytanie jakie właściwosci musi mieć trójkąt równoramienny, aby po połączeniu go z jego bratem bliźniakiem powstał trójkąt równoboczny. Dzięki takim operacjom i pytaniom dzieci znacznie szybciej zaczną rozumieć i trwale pamiętać własności trójkątów.
Zostały nam jeszcze do przetestowania półkwadratusy - czyli inaczej mówiąc trójkąty prostokątne równoramienne, które możemy połączyć na trzy sposoby. I otrzymamy albo duży półkwadratus albo równoległobok... albo też kwadrat! Cuda, które powstają na oczach dzieci nie tyle są zabawą ile pracą, która wykonywana wpływa na ich zrozumienie tego czym są figury o których się uczą. Jest to o tyle istotne, że wprowadzanie właściwości figur i wzorów, bez dobrego zrozumienia tego jak te figury powstają i jakie własności w nich się znajdują, przypomina mi budowanie wielopiętrowego budynku, od piętra trzeciego lub czwartego. A potem się wielce dziwimy (jako rodzice, nauczyciele i edukatorzy), że dzieci po kilku miesiącach (niekiedy tygodniach) nie pamiętają "takich prostych rzeczy". A jak mają pamiętać skoro tego nie odkrywją, nie tworzą i aktywnie nie uczestniczą w procesie tworzenia wiedzy, zrozumienia i łączenia niewidocznych kropek?
Pora na trójkąty równoboczne, bo one mają niesamowite własności. Połączenie dwóch takich gagatków daje nam romb (wcześniej były tylko równoległoboki), zaś trzech - trapez równoramienny. A co by się stało gdybyśmy taki sam trapez dokleili odwracając go do góry nogami? Tak, powstanie właśnie sześciokąt foremny, więc możemy potem zapytać na jakie identyczne figury możemy go podzielić? Odpowiedzi są dość proste: 6 trójkątów równobocznych, 3 romby, 2 trapezy równoramienne oraz jeden sześciokąt foremny. Możemy przy tej okazji krótko powiedzieć o tym, że figury foremne to takie, które mają wszystkie kąty tej samej miary i wszystkie boki tej samej długości. I dzięki temu utrwalimy jeszcze mocniej kwadrat oraz trójkąt równoboczny, jako że obie te figury właśnie są przykładami wielokątów foremnych.
Dobrze byłoby jeszcze pobawić się trójkątami równoramiennymi (nie będącymi półkwadratusami). Jeśli je połączymy ze sobą dłuższymi bokami, to otrzymamy równoległobok lub też deltoid. Natomiast połączenie najkrótszymi bokami sprawi, że ponownie dostaniemy w prezencie romb.
KONCEPCJA 4: Łączenie szachowych koncepcji z interesującymi ciągami: arytmetyczny i geometrycznym.
Zastanówmy się co by się stało, gdybyśmy mieli jeden kwadrat (ten w dolnym, lewym rogu), a potem dokładali jeden ponad nim, a drugi poziomo obok niego. Co by było trzeba zrobić, aby z kwadratów znów powstał (większy) kwadrat? I w ten sposób mamy kwadraty 2x2, 3x3, 4x4, 5x5, 6x6, 7x7 oraz 8x8, który do złudzenia przypomina szachownicę, tyle że bez czarnych (ciemnych) pól. Siatka 8x8 za chwilę będzie służyła nam za pomoc naukową do fajnej sztuczki (jak kto woli pułapki).
Mamy naszą siatkę i teraz malujemy (najlepiej różnymi kolorami), małe kwadraty w następujący sposób. Na najniższym piętrze (warstwie) malujemy jeden kwadrat, na wyższym o jeden więcej (a więc dwa), a potem na każdym wyższym piętrze, znów o jeden więcej niż na poprzednim (niższym). Prosta zabawa, która wydaje się stratą czasu, gdy tymczasem właśnie tworzymy drogę neuronom ku temu, aby się połączyły i pomogły nam zrozumieć zagadnienie ciągów czy jak kto woli ukrytych sekwencji.
Co by się stało gdybyśmy mieli trzy różne kwadraty 2x2, 3x3 i 4x4? W pierwszym z nich malujemy 1x1, w drugim 2x2, a w trzecim 3x3. Co nam pozostaje? Można powiedzieć, że zewnętrzna prawa warstwa, która przypomina literę L. A z ile klocków (małych kwadratów) składa się pierwsza litera, z ilu druga, a z ilu ostatnia? Zapamiętajmy te wartości: 3, 5 i 7, bo za chwilę okażą się naprawdę przydatne. Gotowi?
Weźmy naszą planszę szachową (może też być czysta siatka 8x8). Na najwyższym piętrze (można też zacząć od najniższego), wpisujemy od lewej do prawej (można w odwrotnym kierunku) wartości od 1, powiększając cały czas o 2. Zatem mamy 1, 3, 5, 7, 9, 11, 13, 15. Tutaj zauważamy, że kryje się jakaś stała magiczna liczba, która niewidoczna stoi pomiędzy każdą z par. 1 i 3, 3 i 5, 5 i 7, 7 i 9, etc... różnią się między sobą o dwa. I teraz możemy na wiele sposobów testować szachownicę. Jaka wartość będzie na polu a7, d5, f4 czy h1? A jak obliczyć jaka będzie wartość na danym polu, nie licząc na piechotę? A jak obliczyć ile będzie razem (powiedzmy ziaren piasku), gdy weźmiemy pod uwagę pola od a8 do h8 włącznie? Możliwości jest naprawdę sporo!
Kolejna szachownica jest tym samym co poprzednia, tylko różnica jest taka, że między poszczególnymi liczbami (patrząc i licząc od lewej do prawej) mamy ukrytą liczbę, która powoduje, że kolejne wartości są przewidywalne. Jaka to liczba? Tak jak poprzednio jest to liczba 2, tylko tym razem mnożymy zamiast dodawać. Przykładowo 1*2=2, 2*2=4, 4*2=8, etc. I polecenia oraz zagadki mogą być te same co poprzednio. Pamiętać należy jednak, że wartości mogą być potężne, bo to jest właśnie ukryta lekcja potęgowania dwójki. Dlatego w zależności od narzędzi (np. kalkulatory) i możliwości dzieci, można ograniczyć się do pierwszych dwóch lub trzech rzędów. Wszystko zależy od tego jakie mamy możliwości oraz potrzeby.
Teraz przechodzi do naszych trójkątów równobocznych. Pamiętamy nasze sklejone dwa trapezy, które tworzą sześciokąt foremny. Natomiast trzy trójkąty połączone ze sobą dają nam jeden z takich trapezów. Warto zauważyć, że nie da się stworzyć innej figury z trzej takich trójkątów (zakłądając, że sklejami je bokami).
A co by się stało, gdybyśmy do 1 trójkąta dodali dwa? Otrzymamy oczywiście nasz trapez. A do trapezu gdy dodamy kolejne dwa? (po jednym z obu stron lub oba po jednej stronie)? Wtedy znów otrzymamy trapez (dzieci mogą rozpoznać z nich węża), tyle że nieco dłuższy.
No dobra, ale czemu by nie dodawać trójkątów nad i pod, tylko obok siebie? Spróbujmy zatem tej zabawy. Na początek mamy jeden trójkąt na samej górze, a potem pod nim dodajemy kolejne 3 (jako druga warstwa), tak aby otrzymać znowu trójkąt. Pamiętacie jak prosiłem, aby pamiętać o wartościach 3, 5 i 7? No to dodajmy teraz trzecią warstwę. W drugim trójkącie pierwsza warstwa ma jeden trójkąt, druga trzy, zaś trzecia aż pięć. Natomiast w kolejnym dużym trójkącie dodajemy jeszcze jedną (czwartą) warstwę i mamy 1, 3, 5 i 7. No właśnie: ile razem najmniejszych trójkątów mieści się w każdym z trójkątów? A gdyby trójkąt miał 10, 20, 50 czy 100 warstw? Ile wtedy? No i dalej. Jeśli trójkąt dwuwarstwowy ma 4, trzywarstwowy 9, zaś czterowarstwowy 16, to czy można zauważyć jakąś ukrytą zależność? 2->4, 3->9, 4->16. Wygląda na to, że wyniki są drugą potęgą liczby warstw. 2 do drugiej potęgi to 4, 3 do drugiej daje 9, zaś 4 do potęgi drugiej to oczywiście 16. No i kto powiedział, że matematyka nie może być ukryta w trójkątach?
Na koniec naszej przygody z układaniem identycznych (przystających) figur, możemy zobaczyć obraz, który przedstawia wszystkie możliwości, gdy mamy do dyspozycji półkwadratusy. Przy dwóch możemy je połączyć na 3 sposoby (brakuje równoległoboku), przy trzech - 3 opcje, zaś przy czterach - aż 4. I znowu pojawia się pytanie, które z figur już znamy i jak się one nazywają.
Zawarłem jeszcze specjalny dodatek w prezentacji. Co zawiera?
Pomyślałem, że dobrym pomysłem będzie pokazanie tego w jaki sposób można twórczo przekształcać twierdzenie Pitagorasa. Znowu mamy do dyspozycji proste modele i nożyczki. Pytanie czy kwadrat zielony i czerwony mają taką samą powierzchnię (pole) jak ten fioletowy (ze znakiem zapytania). Następnie zastanówmy się czy trójkąty półkwadratusy: zielony i czerwony będą razem miały to samo pole co fioletowy, a na koniec trójkąty równoboczne: tak samo zielony i czerwony będą razem miały to samo pole co fioletowy. Uważam, że to jest twórcze podejście do odkrywania i udowadniania tego, co może nie być dla wszystkich oczywiste.
A gdyby tak jeszcze na koniec udowodnić klasyczne twierdzenie Pitagorasa, ale tym razem wykorzystując kolorowe trójkąty, które znajdują się w dwóch mniejszych kwadratach? Okazuje się, że to może być doskonale wprowadzenie matematycznej pomocy o nazwie TANGRAM, tak aby pomagać uczniom rozwijać wyobraźnię, a także umiejętności związane z obracaniem i układaniem różnych figur (właśnie tangram jest idealny do tego, aby potem dzieci mogły widzieć "niemożliwe" układy figur).
No i to już koniec prezentacji. Jak widać jest w niej całkiem sporo ciekawych propozycji na to, aby odkrywać i tworzyć matematyczną rzeczywistość. Kluczem do tego jest to, aby dawać dzieciom możliwość operowania na konkretach i sprawdzania oraz poszukiwania tego, co na początku wydaje się nieoczywiste, ukryte i niezrozumiałe. Z czasem można pomagać im w tym, aby mogły przejść na poziom abstrakcyjny w którym cała ich praca oraz jej efekty, zostaną poddane matematycznej obróbce, tak aby mogły operować na wyższym poziomie tym, czego doświadczyły i nauczyły się na niższym poziomach.
Motto, które przyświeca mojej prezentacji jest następujące: jeśli uczniowie nie generują pomysłów i nie tworzą wiedzy, wówczas proces nauki nie jest optymalny. Wierzę w to, że dzieląc się pomysłami oraz możliwościami, które zawarłem w prezentacji, osoby które przeczytają ten artykuł (można do niego wracać wielokrotnie) przekonają się o tym, że matematyka, która daje możliwości odkrywania, tworzenia i dostrzegania tego co na pierwszy rzut oka niewidoczne... jest naprawdę możliwa!