Jak powstaje koło z kwadratu - czyli jak wygląda wnioskowanie na prostych koncepcjach

W poprzednim artykule (na samym końcu) powiedziałem, że niebawem zajmiemy się tym w jaki sposób z prostokąta może powstać trójkąt, zaś z kwadratu... koło! No i teraz czas na odkrycie tego, aby potem stopniowo przejść do tego co się będzie działo, gdy trójkątami jak też naszymi czworokątami zaczniemy obracać, odwracać, przekręcać czy zakręcać. Na razie jednak zobaczmy o co chodzi z tymi dwoma koncepcjami, które wydają się albo niemożliwe albo przynajmniej nieco nieoczywiste. Na pierwszy ogień idzie pierwsza koncepcja (o kole), zaś w następnym kolejna (ta o trójkącie).

Zacznijmy zatem od tego jak z kwadratu może powstać koło (* - zobacz notkę na końcu artykułu).

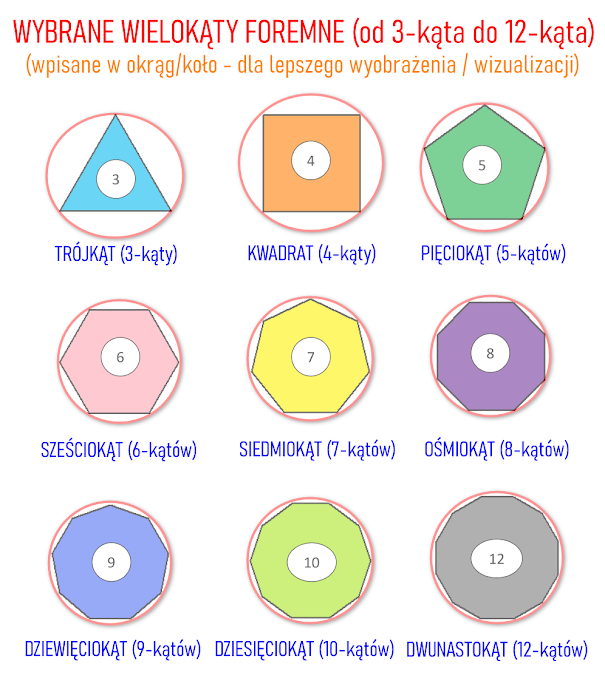
Kwadrat jest przykładem figury zwanej wielokątem foremnym. Każda figura foremna ma dwie cechy: kąty tej samej miary oraz boki tej samej długości.

Zastanówmy się co by się stało, gdybyśmy do naszego czworokąta (kwadratu) dodawali kolejne kąty. Spróbujmy dodawać po dwa kąty do każdej kolejnej figury i zobaczmy co otrzymamy. W takim układzie:

Podkreślam, że cały czas będziemy rozpatrywali wielokąty foremne. Teraz przyjrzyjmy się rysunkom na których widzimy wybrane wielokąty.

Przy okazji warto wiedzieć, że są dwa wzory, które służą do tego, aby obliczyć kąty w wielokątach foremnych.

Pierwszy z nich dotyczy sumy wszystkich kątów wewnętrznych danego wielokąta.

(n*180)-360 = (n-2)*180, przy czym n-liczba kątów (boków) wielokąta, zaś wartości kątów są w stopniach.

Przykładowa suma kątów w trójkącie, kwadracie i sześciokącie będzie wyglądała następująco:

Natomiast wzór na obliczenie kąta wewnętrznego wielokąta foremnego jest następujący:

[(n-2)*180] / n, przy czym n-liczba kątów (boków) wielokąta, zaś wartości kątów są w stopniach. Różnica jest tylko w tym, że najpierw sumujemy wartości wszystkich kątów wewnętrznych (poprzedni wzór), a następnie dzielimy przez liczbę kątów.

W przypadku kolejnych wielokątów tabela dotycząca wartości kąta wewnętrznego wyglądałaby następująco:

Widzimy teraz ciekawą zależność. Mianowicie: im bardziej zwiększamy liczbę kątów (wielokąta foremnego), tym bardziej zwiększa się miara kąta wewnętrznego (w danym wielokącie).

W przypadku 32-kąta, miara jego kąta wewnętrznego to aż 168,75 stopni. Dlaczego to tak ważne? Otóż dlatego, że ten kąt jest bardzo mocno zbliżony do kąta 180 stopni (półpełnego) i właśnie dlatego widząc 32-kąt foremny, prawie każdy stwierdzi, że jest łudząco podobny do koła (a nie do kwadratu czy trójkąta).

Warto również zwrócić uwagę na tempo przyrostu kątów wewnętrznych w zależności od tego z jakim wielokątem foremnym mamy do czynienia (dobrze jest zerknąć na poprzednie tabele). Od 4-kąta do 12-kąta mamy takie oto przyrosty: +30, +15, +9, +6, natomiast od 22-kąta do 32-kąta znacznie mniejsze, bo: +1,15, +0,99, +0,86 i +0,75.

I teraz cała tajemnica się wyjaśnia. Kolejne kąty wewnętrzne (dla wielokątów o coraz większej liczbie kątów) stają się coraz większe, ale już ich miara ("rozwarcia") rośnie coraz wolniej!

Natychmiast nasuwa się kolejne pytanie: a kiedy te kąty wewnętrzne w wielokącie foremnym przestaną rosnąć? (i na jakiej wartości się zatrzymają). Odpowiedź powinna być dość łatwa do przewidzenia. Mianowicie kąty wewnętrzne wielokąta rosną do wartości o której wcześniej wspomnieliśmy, czyli do kąta 180 stopni (półpełnego).

Przykładowo w 10, 100, 1000 i 10000-kącie, owe kąty wewnętrzne będą miały odpowiednio takie miary (w stopniach):

Myślę, że w tym momencie powinno stać się w pełni zrozumiałe, że bez względu na to ile kątów będzie miał nasz wielokąt foremny, to jego kąt wewnętrzny nigdy nie osiągnie wartości kąta półpełnego (180 stopni), chociaż coraz bardziej będzie się do niego zbliżał (wraz ze wzrostem liczby kątów).

A co by było, gdyby jakimś magicznym sposobem ten kąt osiągnął wartość 180 stopni? Wówczas... ten wielokąt przekształciłby się w koło! Z tego rozumowania wynika, że koło to w pewnym sensie nieskończony wielokąt. Pamiętajmy, że jest to oczywiście tylko pewne uproszczenie, mające na celu łatwiejsze zrozumienie zależności pomiędzy wielokątami foremnymi a kołem. Oficjalnie koło NIE JEST wielokątem, zaś wielokąt NIE JEST kołem.

Podsumowując: widzimy wyraźnie co się dzieje, gdy wielokąt foremny zwiększa liczbę kątów: co się dzieje z jego kątem wewnętrznym i jak się ma do koncepcji koła (zarówno wielokąt jak i jego kąt). W ten sposób omówiliśmy "kwadraturę koła" w nieco innej perspektywie. To było nieco inne rozumowanie, jednak wydaje mi się, że na tyle łatwe do zrozumienia, że powinno być w pełni jasne. Kolejnym razem zajmiemy się tym jak z prostokąta wyczarować trójkąt... i jakie są między nimi ciekawe zależności.

[* - notka na końcu artykułu]. W poniższym artykule na końcu (5. Tajemnicza liczba Pi - kwadratura koła) można odrobinę poczytać na temat doświadczenia pod nazwą "kwadratury koła". Mogę powiedzieć, że ten artykuł poniżej był punktem wyjściowym do tego o czy teraz rozmawiamy.

Polecam poświęcić zatem 2-3 minuty na przeczytanie (końcowej części) poprzedniego artykułu - "To jest dobra matematyka - czyli o nauce i sposobach jakie stosować wolno, trzeba a nawet należy (2)" (link poniżej).

https://matmajakiejnieznasz.blogspot.com/2019/12/to-jest-dobra-matematyka-czyli-o-nauce.html