Figury podobne i skala – czyli o tym jak zabawa figurami radość i potencjał wyzwala

W ostatnim artykule omawiającym trójkąty podobne powiedzieliśmy co nieco na temat skali. Dodatkowo pokazaliśmy matematyczny sposób w jaki można sprawdzić czy trójkąty są podobne. Tym razem dodamy do tego sposób praktyczny, czyli ten za pomocą którego będziemy mogli realnie dotknąć skali podobieństwa oraz trójkątów podobnych. Tak, tak – uzasadnianie jest fajne, ale nie wszyscy wierzą na słowo. Dajmy im zatem możliwość samodzielnego sprawdzenia tego czy na pewno trójkąty podobne mają proporcjonalne wymiary i jak te figury na siebie nachodzą oraz czy rzeczywiście mają te same kąty. Zatem zaczynajmy naszą przygodę związaną z testowaniem...

Zastanówmy się na początku jak działa i na czym polega tak naprawdę kserowanie? Czyli mówiąc nieco inaczej: szybkie kserowanie na ekranie, a więc krótka bajka o tym w jaki sposób trójkąt podobny powstanie.

Jeśli dany obiekt (figurę płaską) powiększamy proporcjonalnie, wtedy otrzymujemy obiekt powiększony, ale o tym samym kształcie. To powiększenie zależy od tak zwanego współczynnika. Można powiedzieć, że ten współczynnik to taka magiczna (niewidoczna) soczewka, która może albo powiększać albo pomniejszać dany obiekt.

Taka magiczna soczewka (zwana skalą) powoduje, że obiekt:
a) powiększa się jeśli skala jest większa od 1,
b) pomniejsza się jeśli skala jest mniejsza od 1.

Warto podkreślić, że ta soczewka tworząc figurę podobną, zamienia każdy bok (wymiar) w zależności od liczby (wielokrotności), którą wskazuje skala. Przykładowo skala k=2 oznacza, że każdy bok figury powiększamy dwukrotnie, natomiast k=1/2 – pomniejszamy dwukrotnie.

A co wtedy jeśli skala jest zapisana jako 5:1? Nic trudnego! Otóż wówczas gdybyśmy podzielili te dwie liczby, wtedy otrzymujemy skalę k=5 (inna postać). Analogicznie będzie w przypadku skali 1:5, to znaczy w wyniku dzielenia powstanie skala k=1/5. Przy czym pierwsza skala (wartość) wskazuje powiększenie (większa od jednego), zaś druga – pomniejszenie (bo mniejsza od jednego).

Zobaczmy teraz w jaki sposób możemy wyznaczać figury podobne i odkrywać (obliczać) skalę danej figury. Z uwagi na prostotę i częstotliwość występowania weźmiemy na warsztat trójkąt prostokątny. Pamiętajmy jednak, że tak naprawdę to może być dowolna figura.

Na bazie moich przemyśleń jak też raczej nietypowych analiz (niedostępnych w mądrych księgach matematycznych), doszedłem do wniosku, że najłatwiej będzie wymienić je jedna po drugiej. Od razu dodam, że nie są to wszystkie przypadki, ale na pewno te które uznałem za najbardziej cenne na podstawowym etapie edukacji matematycznej. Tutaj zaczyna się zabawa i przy okazji następuje proces odkrywania i testowania, co oznacza, że proces nauki idzie w dobrym kierunku.

1) Proste równoległe lub prostopadłe do przyprostokątnych.

W pierwszym przypadku wystarczy, abyśmy narysowali dowolne proste, które są równoległe (lub prostopadłe) do krótszej lub dłuższej przyprostokątnej. Bez względu na to gdzie narysujemy taką prostą, odcinek ten stworzy trójkąt podobny do pierwotnego (największego).


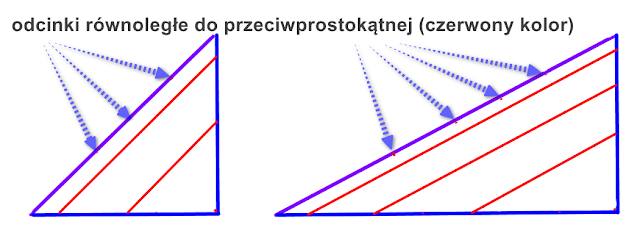
2) Proste równoległe do przeciwprostokątnej.

Tym razem naszym zadaniem jest narysowanie dowolnych prostych, które są równoległe do przeciwprostokątnej. Bez względu na to gdzie narysujemy taką prostą, odcinek ten stworzy trójkąt podobny do pierwotnego (największego).


3) Proste prostopadłe do przeciwprostokątnej.

Następnie naszym zadaniem jest narysowanie dowolnych prostych, które są tym razem prostopadłe do przeciwprostokątnej. Bez względu na to gdzie narysujemy taką prostą, odcinek ten stworzy trójkąt podobny do pierwotnego (największego). Natomiast w przypadku, gdy taki odcinek będzie dodatkowo przechodził przez wierzchołek kąta prostego, wówczas powstaną („jednym cięciem”) dwa trójkąty podobne. Po cichu powiem, że to cięcie często jest wykorzystywane (jak kto woli sprawdzane) w zadaniach dotyczących podobieństwa figur.


4) Proste (i odcinki) związane z przedłużeniem boków figury.

Ostatni ze sposobów polega na rysowaniu przedłużenia boków figury pierwotnej w taki sposób, aby boki najbardziej oddalone od punktu wspólnego obu figur (trójkątów) były do siebie prostopadłe. To dość proste ćwiczenie i jednocześnie wizualnie wciągające.

I teraz najważniejsze. Konieczne jest to aby w procesie nauki tego zagadnienia następowało rysowanie i wycinanie takich podobnych figur. Obowiązkowo musi być także przyłożenie (nałożenie) ich do wspólnego kąta, aby przekonać się i zobaczyć, że pozostałe boki (jak też dodatkowo i kąty!) nakładają się na siebie. Ponadto warto zaznaczyć takimi samymi kolorami te boki (pary boków) które są odpowiednie, a następnie dokonać ich pomiaru. Tak! Koniecznie trzeba ręcznie sprawdzić czy będą tworzyć taką samą proporcję w każdym wypadku. Dopiero wówczas możemy mówić o skali, która jest proporcjonalnym wydłużeniem lub skróceniem każdego z boków według stałej wartości (liczby określającej skalę). Rzecz jasna, takie ćwiczenia można realizować w grupach, gdzie każde dziecko wspólnie odkrywa i testuje matematyczną rzeczywistość.

Podsumowanie: zagadnienie podobieństwa trójkątów warto łączyć ze skalą oraz proporcją. Dzięki temu łatwiej będzie zrozumieć to czym jest owo podobieństwo i na czym polega. Można również pokazywać w jaki sposób drobne zmiany długości dowolnego boku lub kąta sprawia, że przynajmniej jedna proporcja zostanie zaburzona, a więc dany trójkąt (lub inna figura) nie będzie „skserowany” według skali. W wersji dla zaawansowanych można następnie przejść na wyższy poziom, czyli omówić to czym jest i jak się tworzy obraz, gdy mamy jego odbicie i różne przekształcenia. Pomimo tego, że tu już wkraczamy w obszary fizyki (optyka i te sprawy), to jednak dzięki tego typu zajęciom nauka może być wspaniałą twórczą zabawą i stawianiem pytań oraz formułowaniem wniosków… czyli jak dla mnie – najprawdziwszą nauką ze wszystkich możliwych!